Finding Velocity Factor of Unknown Coax

[This topic was originally discussed at the May 2024 Fox Cities Amateur Radio Club meeting.]

For those who missed, the Tech Tip at the May club meeting was determining the velocity factor of an unknown piece of coaxial cable. For those who didn’t, you missed one of Chris’ (N9CVR) famous math errors. We worked a piece of coax out to be 116% velocity factor!

In attempt to redeem the error, here goes another attempt! Chris has a piece of 50-ohm coax which is 16.9ft long. It is unmarked. If we want to use it for normal station use, its electrical length doesn’t really matter. However, there exist applications where its length very much matters!

Larry WA9TT showed one such example. He needed a signal from one of four antennas to arrive at a switching box at exactly the same time. This switching box would then show the operator the direction a signal was coming from.

For the demonstration, Chris used a Jim Williams Pulse Generator (Andy AJ9L had presented about this about a year ago) and an oscilloscope. He connected a tee to the scope. The tee connected to the pulse generator and to one end of the coax. The resulting scope trace looked like this:

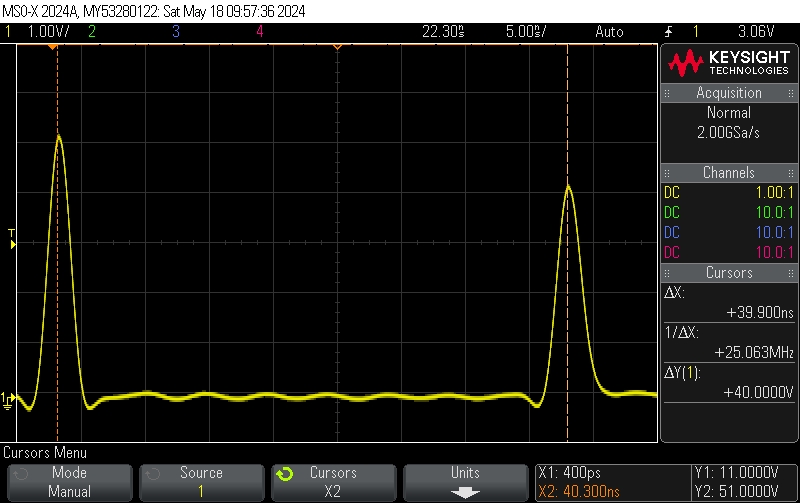
This is called time-domain reflectometry. You can do similar in a large room with a stopwatch by clapping and listening for the echo of the clap. The pulse generator creates the equivalent of a clap, which travels down the coax, and bounces back off the end, into the oscilloscope.

The left pulse came from the pulse generator, and the smaller right pulse was a reflection from the end of the coax. Total time from the pulse to its reflection is 39.9 nanoseconds.

Here’s where the math comes in – Electricity theoretically travels at the speed of light – about 300 million meters per second. Using this information, we can calculate the coax’ apparent length:

$L_{app} = \frac{299,792,458[m/s] \times 0.398 [\mu s]}{2\times 10^{6}[\mu s]} = 5.891 [m] = 19.623[ft]$

But we measured the coax to be 16.9ft long.

$VF [\%] = \frac{L_{act}}{L_{app}} \times 100 [\%] = \frac{16.9[ft]}{19.6[ft]} \times 100 [\%] = 86.2 [\%]$

Hopefully this little math trick helps you next time you’re building an antenna or trying to identify a random unmarked piece of transmission line!